Compiler Design [7]

2009 Oct 18

Compiler Phases

Lexical Analysis
Syntactic Analysis
Intermediate Code Generation
Code Optimization
Code Generation
Support

Table Management
Error Handling
Program
  • Data
    • Data - declarations
    • Heap - dynamic
    • Stack - code linkages
  • Functions
    • Blocks
      • Declarations
      • Statments
        • Control Flow
        • Expressions
        • Data references
        • Function calls

Lexical
FSM		 Operator
Associativity
NFA2DFA.ppt RE2NFA2DFA.pdf

Lexical Finite State Machines

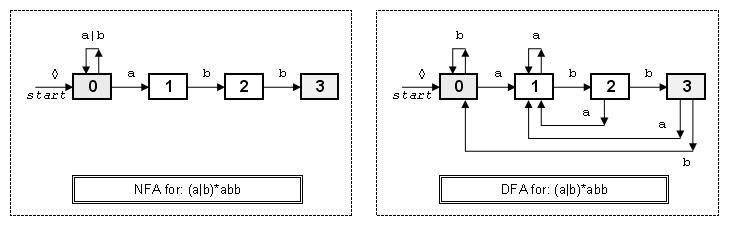
A FSM can be either deterministic (DFA) or nondeterministic (NFA). For the regular expression: (a|b)*abb it is easy to construct the following NFA (where the green state is the single start state and blue states are final or accepting states (in general there can be more than one). Transitions are labeled with the character set that they recognize. A special symbol, ◊, is used to label an empty transition; i.e. one which takes place without an input character being consumed. It is always possible to construct a DFA for any NFA, although the number of states in the resulting DFA could be exponential.

The algorithm to convert a NFA to a DFA is often called Subset Construction.

Input: An NFA, N, specified as a list of states (with special start state 0), where each state has a list of input characters (including ◊). Associated with this list of input characters is the list of states, for each input character, that input will (nondeterninistically) transition to. For the above example this is:

0; a{0, 1}, b{0}
1; b{2}
2; b{3}
3+; // the plus marks state 3 as an accepting state
Output: A DFA, D, also accepting N's language.

Algorithm: Each state of D is a set of states which N could be in after reading some sequence of input symbols, thus simulating in parallel all possible moves, or state transitions, N can make on a given input string. The initial state of D is the set of consisting of s0 (from N along with all states of N reachable by ◊ transitions.

The function closure(s) is defined to be the set of states of N build by appling the following rules:

  1. s is added to closure(s)
  2. if t is in closure(s), and there is a transition labeled ◊ from t to u then u is added to closure(s) if u is not already there. Rule 2 is repeated until no more states can be added to closure(s).

Thus closure(s) is just the set of states that can reached from s on ◊ transitions alone.

The states of D and their transitions are constructed as follows. Initially, let closure(s0) be a state of D - this is the start state of D. Initially every state of D is unmarked. Then perform the subset algorithm:

subset() {
    while there is an unmarked state x={s1, s2, ... } of D do {
        mark x;
        for each input symbol a {
            Let T be the set of states to which there is a transition on a 
                from state si in x;
            y := closure(T);
            if y has not yet been added to set of states of D
                then make y an unmarked state of D;
            Add a transition from x to y labeled a if not
                already present;
        }
    }	
}

Operator Associativity

a + b + c

Left  Associative: ( ( a + b ) + c ) )
Right Associative: ( ( a + ( b + c ) )
Operator associativity is fundamental for unary operators,

2007-2009