



Next: CONTEXT-FREE LANGUAGES
Up: Limitations of Regular Languages
Previous: Limitations of Regular Languages
Contents
Consider the following three languages:
The first language is regular, since it contains only a finite number
of strings.
The third language is also regular, since it is equivalent to the
regular expression (a*)(b*).
The second language consists of all strings which contain a number of
`a's followed by an equal number of `b's.
Lemma: 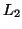 is not regular
is not regular
Strategy: Proof by contradiction
Proof: Let us assume that it is regular; then we must
have some set of strings of the form
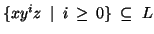 .
.
Suppose such a subset did exist.
- -
- Obviously,
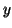 could not contain a mixture of `a's and `b's,
since this would mean that
could not contain a mixture of `a's and `b's,
since this would mean that 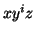 would have `b's before `a's. Thus,
would have `b's before `a's. Thus,
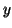 must consist solely of `a's or solely of `b's.
must consist solely of `a's or solely of `b's.
- -
- Let us assume then that
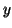 consists solely of `a's. Then if, for some
consists solely of `a's. Then if, for some 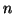 we have that
we have that 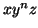 is in
the language, there is no way that
is in
the language, there is no way that 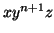 can be in the language,
since this will contain extra `a's without any extra `b's. Thus there
will be no way for
can be in the language,
since this will contain extra `a's without any extra `b's. Thus there
will be no way for 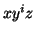 to be in the language for every
to be in the language for every 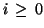 .
.
- -
- We can use exactly the same argument to refute the supposition that
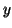 can consist entirely
of `b's.
can consist entirely
of `b's.
Thus we have shown that 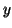 cannot consists of `a's `b's or their
mixture; ie no such
cannot consists of `a's `b's or their
mixture; ie no such 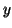 exists, and so the Pumping Lemma is not
satisfied. Thus
exists, and so the Pumping Lemma is not
satisfied. Thus 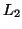 is not regular.
is not regular.
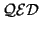
(Note that we cannot draw any conclusions from the fact that
 ).
).




Next: CONTEXT-FREE LANGUAGES
Up: Limitations of Regular Languages
Previous: Limitations of Regular Languages
Contents
James Power
2002-11-29
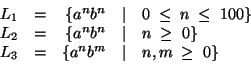
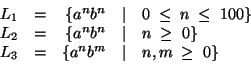
![]() is not regular
is not regular
![]() .
.
![]() ).
).