The Chomsky Hierarchy

Obviously languages exist which are not regular; Noam Chomsky categorised regular and other languages as follows:

Language Class	Grammar	Automaton
3	Regular	NFA or DFA
2	Context-Free	Push-Down Automaton
1	Context-Sensitive	Linear-Bounded Automaton
0	Unrestricted (or Free)	Turing Machine

This is a hierarchy, so every language of type 3 is also of types 2, 1 and 0; every language of type 2 is also of types 1 and 0 etc.

The distinction between languages can be seen by examining the structure of the production rules of their corresponding grammar, or the nature of the automata which can be used to identify them.

• Type 3 - Regular Languages
  

  As we have discussed, a regular language is one which can be represented by a regular grammar, described using a regular expression, or accepted using an NFA or a DFA.
  

• Type 2 - Context-Free Languages
  

  A Context-Free Grammar (CFG) is one whose production rules are of the form:
  

  $$\begin{array}{rcl} A & \rightarrow & \alpha \\ \end{array}$$
  
  

  where $A$ is any single non-terminal, and $\alpha$ is any combination of terminals and non-terminals.
  

  A NFA/DFA cannot recognise strings from this type of language since we must be able to "remember" information somehow. Instead we use a Push-Down Automaton which is like a DFA except that we are also allowed to use a stack.
  

• Type 1 - Context-Sensitive Languages
  

  Context-Sensitive grammars may have more than one symbol on the left-hand-side of their production rules (provided that at least one of them is a non-terminal). However, the production rules must now obey the following:

  CS1

  The number of symbols on the left-hand-side must not exceed the number of symbols on the right-hand-side

  CS2

  We do not allow rules of the form 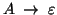$A\; \rightarrow\; \varepsilon$ unless 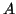$A$ is the start symbol and does not occur on the right-hand-side of any rule.

  Since we allow more than one symbol on the left-hand-side, we refer to those symbols other than the one we are replacing as the context of the replacement.
  

  The automaton which recognises a context-sensitive language is called a linear-bounded automaton: this is basically a NFA/DFA which can store symbols in a list.
  

  Conditions CS1 and CS2 above mean that the sentential form in any derivation must always increase in length every time a production rule is applied. This basically means that the size of a sentential form is bounded by the length of the sentence (ie. word) we are deriving.
  

  Since the sentential form cannot thus grow infinitely large before deriving a sentence, a linear-bounded automaton always uses a finitely-long list as its store.
  

• Type 0 - Unrestricted (Free) Languages
  

  Free grammars have absolutely no restrictions on their grammar rules, (except, of course, that there must be at least one non-terminal on the left-hand-side).
  

  The type of automata which can recognise such a language is basically a NFA/DFA with an infinitely-long list at its disposal to use as a store; this is called a Turing machine.