Eliminating Indirect Left Recursion

Indirect left recursion occurs as follows:

Suppose we have non-terminals $A_0, A_1, \ldots, A_n$ and that $\alpha_1, \alpha_1, \ldots, \alpha_{n+1}$ are mixtures of terminals and non-terminals, then the production rules:

$$\begin{array}{rcl} A_0 & \rightarrow & A_1 \alpha_1\; \mid\; ... ... \rightarrow & A_0 \alpha_{n+1}\; \mid\; \ldots \\ \end{array}$$

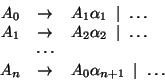
could result in a leftmost derivation of the form:

$$\begin{array}{ccccccccc} A_0 & \rightarrow & A_1 \alpha_1 & \... ...htarrow & A_0 \alpha_{n+1} \ldots \alpha_2 \alpha_1 \end{array}$$

Again, such a derivation would cause problems during a top-down parse.

If we have a grammar that does not have a derivation of the form $B\; \rightarrow^*\; B$, for any non-terminal $B$ (ie. the grammar has no cycles), and there are no $\varepsilon$-productions, then we can apply the following algorithm to eliminate all left recursion.

Let $\alpha, \beta_1, \ldots,\beta_n$ represent any mixture of terminals and non-terminals. Then:

1. Arrange all the non-terminals into some arbitrary order: call them $A_1, A_2, \ldots, A_n$

2. For each non-terminal $A_i$ in turn, do:
   1. For each terminal $A_i$ such that $1 \leq j < i$ and we have a production rule of the form $A_i\, \rightarrow\, A_j \alpha$, where the $A_j$ productions are $A_j\, \rightarrow\, \beta_1\, \mid\, \ldots\, \mid\, \beta_n$, do:
      Replace the production rule $A_i\; \rightarrow\; A_j\alpha$ with the rule $A_i\, \rightarrow\, \beta_1 \alpha\, \mid\, \ldots\, \mid\, \beta_n \alpha$
   2. Eliminate any immediate left recursion among the $A_i$ productions

This algorithm is preventative in nature - it does not look for left recursion and then eliminate it; instead, it rearranges the grammar so that no left recursion can possibly occur. Thus, even non-left-recursive grammars may be rewritten using this algorithm.

The effect of step 2(a) above is to eliminate all production rules of the form $A_i\; \rightarrow\; A_j\alpha$ for every $j\, <\, i$; in other words, if we have a chain of derivations of the form:

$$\begin{array}{ccccccccc} A_0 & \rightarrow & A_1 \alpha_1 & ... ...\rightarrow & A_i \alpha_i \ldots \alpha_2 \alpha_1 \end{array}$$

We can be sure that the index $i$ of $A_i$ is increasing all the time, and so can never get back around to 0 at any stage in the derivation (which would have caused recursion).

Note:

the replacement technique used in step 2(a) is a standard procedure: if we ever have a production rule involving a non-terminal on the r.h.s. that we ``don't like'' for some reason,then we get rid of it by replacing it in the rule with the r.h.s. of its production rule(s).