Unger's Method

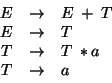
When faced with a choice of production rules, Unger's Method works by evaluating all possible partitions of the input string that can correspond to the symbols on the right-hand-side of each option.

As an example, we take the grammar

$$\begin{array}{rcl} E & \rightarrow & E\; +\; T \\ E & \right... ...& \rightarrow & T\; * a \\ T & \rightarrow & a \\ \end{array}$$

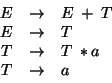
Suppose we are trying to match the string ``a$\ast$a+a''.

We may represent the initial situation as an attempt to match $E$ to this:

$$\begin{array}{\vert c\vert} \hline E \\ \hline a*a+a \\ \hline \multicolumn{1}{c}{Table\; 1} \\ \end{array}$$

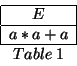
As there are two options for the right-hand-side, we enumerate these as:

$$\begin{array}{\vert c\vert c\vert c\vert} \hline E & + & T ... ...*a+a \\ \hline \multicolumn{1}{c}{Table\; 1.2} \\ \end{array}$$

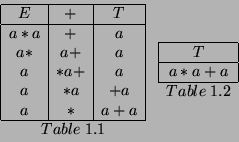
If we consider table 1.2 first, we can expand the production rules for $T$ to get two new tables:

$$\begin{array}{\vert c\vert c\vert c\vert} \hline T & * & a ... ...a+a \\ \hline \multicolumn{1}{c}{Table\; 1.2.2}\\ \end{array}$$

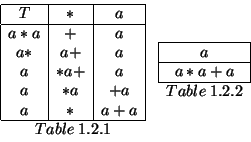
Now by just looking at the columns involving terminal symbols, we can tell that both of these are impossible. The only correct rows in table 1.2.1 should have a ``$\ast$'' in the second column and an ``a'' in the third: there are none. Similarly, in table 1.2.2 it is clearly impossible for ``a'' to be the same as ``a$\ast$a+a'', and so we reject this also.

Going back then to table 1.1, we can see that some of its rows can also be eliminated. The middle column has the terminal ``+'' in it, so the only acceptable rows are those with a ``+'' in this column: that is row 1. So the table now looks like:

$$\begin{array}{\vert c\vert c\vert c\vert} \hline E & + & T \\ \hline a*a & + & a \\ \hline \end{array}$$

Now for each row that is left, we must expand both $E$ and $T$, and consider their possible partitions.

Since we know that $T$ can generate ``a'' (we could write out the tables to prove this), we can proceed with analysing $E$. Expanding out we get:

$$\begin{array}{\vert c\vert c\vert c\vert} \hline E & + & T \... ...*a \\ \hline \multicolumn{1}{c}{Table\; 1.1.2} \\ \end{array}$$

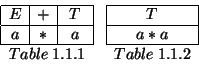
We can throw away table 1.1.1 immediately since ``+'' won't match with ``$\ast$''. Expanding the remining table gives us

$$\begin{array}{\vert c\vert c\vert c\vert} \hline T & * & a \... ... \\ \hline \multicolumn{1}{c}{Table\; 1.1.2.2} \\ \end{array}$$

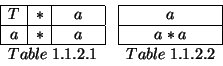
The second table can be thrown away, and expanding $T$ shows that table 1.1.2.1 does indeed represent a correct parse.