



Next: Closure of Regular Languages
Up: Further Properties of Regular
Previous: Further Properties of Regular
Contents
The last type of FSA that we need to look at is the total DFA -
this has properties which we will need in the next section.
A total FSA is one where each state has exactly one transition to some
other state for every input symbol. Thus there are no ``gaps''
in the transition table for the machine: given any state and any input
symbol, it will always be possible to make a transition.
We can convert any ordinary DFA to a total DFA as follows:
- Create some new state
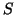 , which we will use for ``stuck''
computations
, which we will use for ``stuck''
computations
- For each input symbol, make a transition from state
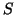 to
itself: thus it is never possible to leave this state.
to
itself: thus it is never possible to leave this state.
- For each other state
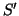 , and for every possible input symbol
, and for every possible input symbol
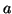 , check to see if
, check to see if 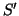 has an outgoing transition on
has an outgoing transition on 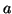 ; if it
doesn't, then make a new transition from
; if it
doesn't, then make a new transition from 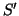 to
to 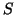 on
on 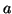 .
.
It can be easily seen that this DFA is total.




Next: Closure of Regular Languages
Up: Further Properties of Regular
Previous: Further Properties of Regular
Contents
James Power
2002-11-29