



Next: Other Decision Problems for
Up: Further Properties of Regular
Previous: Total DFA
Contents
By the definition of regular expressions (and by Thompson's
algorithm), we know that the union, concatenation and Kleene closure of
regular languages must also be a regular language.
It is reasonable to ask: does this hold for other ``set-theoretic'' operations,
such as intersection, difference and complement? We prove that these
languages are regular by constructing the appropriate automata.
Let 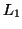 and
and 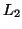 be regular languages over the alphabet
be regular languages over the alphabet 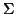 , and let
, and let
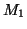 and
and 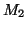 be their corresponding total DFAs.
be their corresponding total DFAs.
Let us define the components of 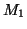 and
and 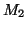 as follows:
as follows:
- let the set of states of
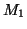 be
be 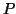 , from which we distinguish:
, from which we distinguish:
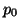 , the start state of
, the start state of 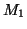
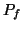 , the set of final states of
, the set of final states of 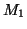
- let
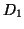 be the transition function for
be the transition function for 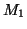 ; that is, the
(partial) function:
; that is, the
(partial) function:
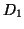 :
:
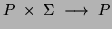
- let the set of states of
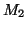 be
be 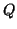 , from which we distinguish:
, from which we distinguish:
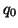 , the start state of
, the start state of 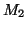
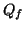 , the set of final states of
, the set of final states of 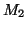
- let
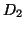 be the transition function for
be the transition function for 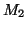 ; that is, the
(partial) function:
; that is, the
(partial) function:
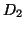 :
:
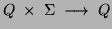
Now we can define:
- The intersection of
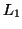 and
and 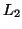 is the machine
is the machine 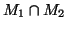 defined by:
defined by:
- the set of states is
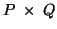 , the Cartesian product of
, the Cartesian product of 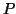 and
and 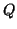 .
Thus for any
.
Thus for any 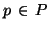 and
and 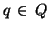 , the pair
, the pair 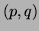 is a state.
We distinguish:
is a state.
We distinguish:
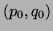 , the start state of
, the start state of 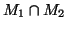
-
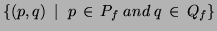 ,
the set of final states of
,
the set of final states of 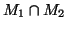
- the transition function:
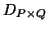 :
:
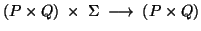 is defined, for any character `a', by:
is defined, for any character `a', by:
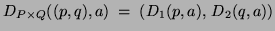
- The difference of
 and
and 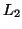 is the machine
is the machine 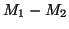 , defined
as for intersection, except that the set of final states is now:
, defined
as for intersection, except that the set of final states is now:
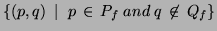
- The complement of the language
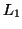 is the machine
is the machine 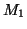 ', which is
simply
', which is
simply 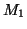 with the final and non-final states swapped; ie. the set of final
states is:
with the final and non-final states swapped; ie. the set of final
states is: 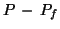




Next: Other Decision Problems for
Up: Further Properties of Regular
Previous: Total DFA
Contents
James Power
2002-11-29
![]() and
and ![]() be regular languages over the alphabet
be regular languages over the alphabet ![]() , and let
, and let
![]() and
and ![]() be their corresponding total DFAs.
be their corresponding total DFAs.
![]() and
and ![]() as follows:
as follows: