Grammars

Basically, a grammar consists of a set of production rules of the form:

$$\begin{array}{rcl} A & \rightarrow & \alpha \\ \end{array}$$

where $A$ is a symbol known as a non-terminal, and $\alpha$ is a sequence of symbols.

Each production rule can be seen as giving the definition of the non-terminal on the left-hand-side; the above rule states that ``whenever we see an $A$, we can replace it with $\alpha$''.

A non-terminal may have more than one definition, in which case we use ``$\mid$'', the union operator; eg.

$$\begin{array}{rcl} A & \rightarrow & \alpha \\ & \mid & \beta \\ \end{array}$$

means that ``whenever we see an $A$, we can replace it with $\alpha$ or with $\beta$''.

We distinguish one special non-terminal in the grammar called the start symbol, usually written $S$. The production rules for this symbol are usually written first in a grammar.

Any symbol used in the grammar which does not appear on the left-hand-side of some rule (ie. has no definition) is called a terminal symbol.

The following is an example of a grammar:

$$\begin{array}{rcl} S & \rightarrow & X {\bf c} \\ X & \right... ...Y & \rightarrow & {\bf a} \\ & \mid & {\bf b} \\ \end{array}$$

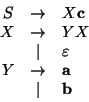
The non-terminals of the grammar are $S$, $X$ and $Y$; the terminals are a, b, c.

A grammar works by starting with the start symbol, and successively applying the production rules (replacing the l.h.s. with the r.h.s.) until we get a word which contains no non-terminals; this is known as a derivation.

Anything which we can derive from the start symbol by applying the production rules is called a sentential form. The last sentential form which contains no non-terminals is called a sentence.

Note that any grammar may have an infinite number of sentences which can be derived; the set of all these sentences is the language defined by the grammar.

Some experimentation with the above grammar will show that it can derive all words which start with arbitrarily many `a's or `b's and finish with a `c' - this is the language defined by the regular expression (a|b)*c.

In fact, every regular expression can be converted to a grammar.

However, not every grammar can be converted back to a regular expression; any grammar which can is called a regular grammar; the language it defines is a regular language.

$$\begin{array}{rcl} Regular\; Expression & \longrightarrow & G... ...Expression & \longleftarrow & Regular\; Grammar \\ \end{array}$$