



Next: Grammars
Up: Further Properties of Regular
Previous: Closure of Regular Languages
Contents
We use a FSA to answer a question of the form: ``is 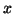 in the language
in the language 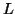 ?''.
This is known as a decision problem, since the answer will be ``yes'' or ``no''.
We can pose other decision problems for regular languages:
?''.
This is known as a decision problem, since the answer will be ``yes'' or ``no''.
We can pose other decision problems for regular languages:
- DP1
- For any regular language
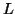 , is
, is
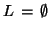 ?
?
- DP2
- For any two regular languages
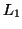 and
and 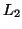 , is
, is
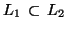 ?
?
- DP3
- For any two regular languages
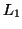 and
and 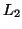 , is
, is 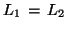 ?
?
Once again, we approach these problems by examining the corresponding FSAs.
The corresponding FSA decision problem, and the decision algorithm, for the above are:
- DP1
- Given a FSA
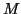 , does
, does 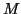 accept any strings?
accept any strings?
A FSA accepts no strings if either there are no final states, or if there is
no path from the start state to a final state. To see if this is so, we need
to work out which states are ``reachable'' from the start state. Construct
the following sets of states:
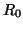 just contains the start state
just contains the start state
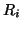 is all the states in
is all the states in 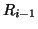 , along with any states
reachable in one transition from a state in
, along with any states
reachable in one transition from a state in 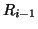
We stop the construction when
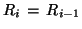 (this has to happen, as
there are only a finite number of states altogether). When this
happens, just examine the states in
(this has to happen, as
there are only a finite number of states altogether). When this
happens, just examine the states in 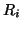 ; if this set doesn't contain any
final states, then
; if this set doesn't contain any
final states, then 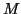 accepts no strings.
accepts no strings.
- DP2
- Given two FSAs
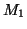 and
and 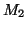 , is the language accepted by
, is the language accepted by 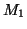 a
subset of that accepted by
a
subset of that accepted by 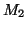 ?
?
We note that
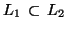 if and only if
if and only if
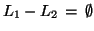 .
Thus our algorithm is: construct the machine
.
Thus our algorithm is: construct the machine 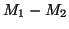 (as in the last
section), and apply the algorithm for
(as in the last
section), and apply the algorithm for ![$[DP1]$](img79.png)
- DP3
- Given two FSAs
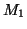 and
and 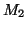 , is the language accepted by
, is the language accepted by 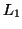 equal to that accepted by
equal to that accepted by 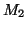 ?
?
We note that 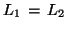 if and only if they are subsets of each other.
Thus we simply apply
if and only if they are subsets of each other.
Thus we simply apply ![$[DP2]$](img80.png) twice.
twice.




Next: Grammars
Up: Further Properties of Regular
Previous: Closure of Regular Languages
Contents
James Power
2002-11-29
![]() in the language
in the language ![]() ?''.
This is known as a decision problem, since the answer will be ``yes'' or ``no''.
We can pose other decision problems for regular languages:
?''.
This is known as a decision problem, since the answer will be ``yes'' or ``no''.
We can pose other decision problems for regular languages: