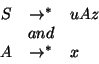Repetition in a CFG is achieved by recursion in the rules. This can occur directly or indirectly, but will result in a derivation of the form:
Each time we apply the sequence of rules which recurse back to
This ``matching'' or ``balancing'' of two patterns is the hallmark of context-free languages.
This can be broken down into two sub-questions:
- For what sort of parse tree does this ``pumping'' happen?
If a derivation ``pumps'' on some non-terminal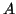 , then this
non-terminal must occur twice in some path from the root of the parse
tree to one of the leaves. This is guaranteed to happen if we know
that the grammar has, say,
, then this
non-terminal must occur twice in some path from the root of the parse
tree to one of the leaves. This is guaranteed to happen if we know
that the grammar has, say, 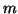 non-terminals altogether, and the parse
tree for a string has a path with length greater than
non-terminals altogether, and the parse
tree for a string has a path with length greater than 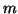 (we simply
run out of non-terminals to label the nodes with, and so must repeat
one!). So a parse tree contains a ``pump'' if its height is greater
than
(we simply
run out of non-terminals to label the nodes with, and so must repeat
one!). So a parse tree contains a ``pump'' if its height is greater
than 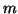 .
.
- For what sort of strings does this ``pumping'' happen?
Suppose the maximum number of symbols on the r.h.s. of any grammar rule of the language is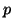 . Then each application of any rule
generates at most
. Then each application of any rule
generates at most 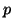 symbols; (ie. each node of the parse tree has at
most
symbols; (ie. each node of the parse tree has at
most 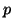 children). Thus a path of length
children). Thus a path of length 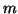 or less can generate at
most
or less can generate at
most 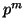 symbols. This means that if we have a string of length
greater than
symbols. This means that if we have a string of length
greater than 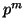 , there must have been a ``pump'' in the parse tree
which generated it.
, there must have been a ``pump'' in the parse tree
which generated it.