



Next: The Pumping Lemma: Examples
Up: Proving that a Language
Previous: Proving that a Language
Contents
For any context-free grammar 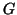 , there is a number
, there is a number 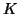 , depending on
, depending on 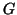 , such that
any string generated by
, such that
any string generated by 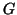 which has length greater than
which has length greater than 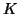 can be written in
the form
can be written in
the form 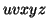 , so that either
, so that either 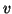 or
or 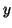 is non-empty, and
is non-empty, and 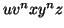 is
in the language generated by
is
in the language generated by 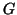 for all
for all 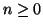 .
.
Proof:
Based on the above discussion, we can see that the number 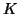 is simply
is simply 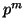 .
.
James Power
2002-11-29