The Closure of Context-Free Languages

We have seen that the regular languages are closed under common set-theoretic operations; the same, however, does not hold true for context-free languages.

Lemma: The context-free languages are closed under union, concatenation and Kleene closure.
That is, if $L_1$ and $L_2$ are context-free languages, so are $L_1 \cup L_2$, $L_1 L_2$ and $L_1^*$.
Proof:
We will prove that the languages are closed by creating the appropriate grammars.
Suppose we have two context-free languages, represented by grammars with start symbols $S_1$ and $S_2$ respectively. First of all, rename all the terminal symbols in the second grammar so that they don't conflict with those in the first. Then:

• To get the union, add the rule $S\; \rightarrow\; S_1\; \mid\; S_2$
• To get the concatenation, add the rule $S\; \rightarrow\; S_1\; S_2$
• To get the Kleene Closure of $L_1$, add the rule $S\; \rightarrow\; S_1\; S \mid\; \varepsilon$ to the grammar for $L_1$.

${\cal QED}$

Lemma: The context-free languages are not closed under intersection
That is, if $L_1$ and $L_2$ are context-free languages, it it not always true that $L_1 \cap L_2$ is also.
Proof:
We will prove the non-closure of intersection by exhibiting a counter-example.
Consider the following two languages:

$$\begin{array}{lcrcl} L_1 & = & \{a^ib^jc^k & \mid & i < j\} \\ L_1 & = & \{a^ib^jc^k & \mid & i < k\} \\ \end{array}$$

We can prove that these are context-free by giving their grammars:

$$\begin{array}{lrcl} L_1 = & S & \rightarrow & ABC \\ & A & ... ... & C & \rightarrow & {\bf c}C\; \mid\; {\bf c} \\ \end{array}$$

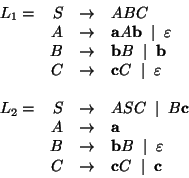
The intersection of these languages is:

$$\begin{array}{lcrcl} L_1 \cap L_2 & = & \{a^ib^jc^k & \mid & i < j\; and\; i < k\} \\ \end{array}$$

We proved in the last section that this language is not context-free.
${\cal QED}$

Lemma: The context-free languages are not closed under complementation.
That is, if $L$ is a context-free language, it it not always true that $L'$ is also.
Proof: (By contradiction)
Suppose that context-free languages are closed under complementation.
Then if $L_1$ and $L_2$ are context-free languages, so are $L_1'$ and $L_2'$. Since we have proved closure under union, $(L_1' \cup L_2')$ must also be context-free, and, by our assumption, so must its complement $(L_1' \cup L_2')'$.
However, by de Morgan's laws (for sets), $(L_1' \cup L_2')' \equiv (L_1 \cap L_2)$, so this must also be a context-free language.
Since our choice of $L_1$ and $L_2$ was arbitarary, we have contradicted the non-closure of intersection, and have thus proved the lemma.
${\cal QED}$