



Next: TOP-DOWN PARSING
Up: CONTEXT-FREE LANGUAGES
Previous: The Closure of Context-Free
Contents
Based on the Pumping Lemma, we can state some decidability results for
context-free languages.
Lemma: It is decidable whether or not a given string belongs to a
context-free language.
Proof:
If we eliminate all 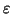 -productions, and all unit productions
from the context-free grammar for the language, then each time we apply
a production rule we either:
-productions, and all unit productions
from the context-free grammar for the language, then each time we apply
a production rule we either:
- -
- make the sentential form grow longer
- -
- increase the number of terminal symbols in the sentential form
Therefore the number of production rules applied (and thus the height of the
parse tree) will be bounded by the length of the input string. Since this is
finite, an effective (though inefficient) decision algorithm need only
enumerate all such parse trees, and check the leaves to see if they correspond
to the string.
Without examining the issue in detail, we also note the following:
- The constraints placed on the rule-format of context-sensitive grammars allow
us to use the same argument as above to assert that language membership is
decidable.
- In order to decide if a string is a member of a free language, we
run the corresponding Turing Machine, and see if it halts on ``yes''. Clearly
this is the Halting Problem, which is undecidable. Thus it is not
possible in general to construct a parser for a free language.
Lemma: It is decidable whether or not a context-free language is empty.
Proof:
We need to show that the corresponding context-free grammar can generate a string.
If a CFG can generate a string, then it should be able to do so without using
recursion (since we could just skip the recursion and generate a shorter string).
If there are 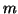 non-terminals altogether, then some tree of height less than
non-terminals altogether, then some tree of height less than
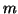 must have leaves which are only terminals.
must have leaves which are only terminals.
Thus we need only examine all such trees to see if the CFG generates a sentence.
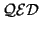
Some decision problems for CFGs (and accordingly for push-down automata)
are not solvable.
We state, without proof, that the following problems are undecidable in general:
- Given two context-free languages
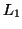 and
and 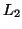 , is
, is
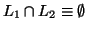 ?
?
ie. do two context-free grammars generate the same string?
- Given some alphabet of terminal symbols
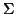 , does a grammar over
this alphabet generate all the strings of
, does a grammar over
this alphabet generate all the strings of 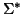 ?
?
- Is the context-free grammar for a language ambiguous?
- Given two context-free languages
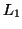 and
and 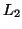 , is
, is
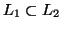 ?
?
- Given two context-free languages
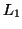 and
and 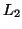 , is
, is 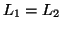 ?
?
The proof of these theorems follows from a famous decision problem called
Post's correspondance problem.




Next: TOP-DOWN PARSING
Up: CONTEXT-FREE LANGUAGES
Previous: The Closure of Context-Free
Contents
James Power
2002-11-29
![]() -productions, and all unit productions
from the context-free grammar for the language, then each time we apply
a production rule we either:
-productions, and all unit productions
from the context-free grammar for the language, then each time we apply
a production rule we either:
![]() non-terminals altogether, then some tree of height less than
non-terminals altogether, then some tree of height less than
![]() must have leaves which are only terminals.
must have leaves which are only terminals.
![]()