



Next: FIRST and FOLLOW
Up: TOP-DOWN PARSING
Previous: Recursive Descent Parsing
Contents
The basic problem in parsing is choosing which production rule to use
at any stage during a derivation. Any approach to parsing which
involves backtracking will probably involve creating complex or
inefficient algorithms in a conventional programming language. To
make implementation easier, we introduce the notion of lookahead.
- Lookahead
- means attempting to analyse the possible production rules which
can be applied, in order to pick the one most likely to derive the current
symbol(s) on the input.
Suppose we are in the middle of a derivation, where we have:
- Current Sentential Form =
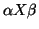
- Input string =
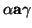
where:
- -
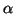 consists entirely of terminals, and corresponds to the piece of
the input that has already been matched
consists entirely of terminals, and corresponds to the piece of
the input that has already been matched
- -
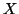 is the leftmost non-terminal,
is the leftmost non-terminal, 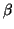 is the rest of the sentential form
is the rest of the sentential form
- -
- a is the next symbol on the input,
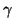 is the rest of the input
is the rest of the input
Our job then is to figure out which production rule will allow 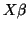 can derive
can derive
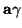 ; thus we examine the r.h.s. of the production rules for
; thus we examine the r.h.s. of the production rules for 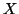 as follows:
as follows:
- If the r.h.s. starts with a terminal symbol, then it must be of the form
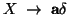 for this rule to be of any use
for this rule to be of any use
- If the r.h.s. starts with a non-terminal, ie. it looks like
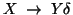 say, then
say, then
- we must examine the production rules for
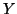 to see if any of these can derive an a.
to see if any of these can derive an a.
- If
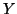 can derive
can derive 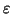 , then we must see what
, then we must see what 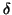 can derive;
ie. apply steps 1 and 2 to the production rules for
can derive;
ie. apply steps 1 and 2 to the production rules for 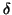 .
.
- If we find that
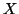 can derive
can derive 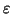 , then we must check to see what
the symbols following
, then we must check to see what
the symbols following 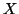 in the sentential form (ie. the first symbol in
in the sentential form (ie. the first symbol in 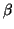 )
can derive.
)
can derive.
Subsections




Next: FIRST and FOLLOW
Up: TOP-DOWN PARSING
Previous: Recursive Descent Parsing
Contents
James Power
2002-11-29
![]() can derive
can derive
![]() ; thus we examine the r.h.s. of the production rules for
; thus we examine the r.h.s. of the production rules for ![]() as follows:
as follows: