Also,
-
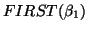 is in
is in
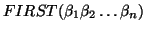
if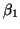 can derive
can derive 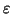 , then
, then
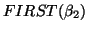 is also in
is also in
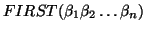
if both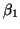 and
and 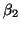 can derive
can derive 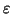 , then
, then
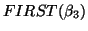 is also in
is also in
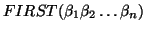
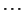
if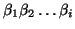 can derive
can derive 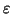 , then
, then
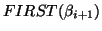 is also in
is also in
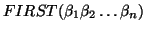
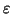 is in
is in
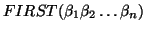 only if
only if 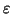 is in
is in
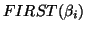 , for all
, for all
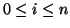
We formalise the task of picking a production rule using two functions, FIRST and
FOLLOW.
FIRST is applied to the r.h.s. of a production rule, and tells us all the terminal symbols that can start sentences derived from that r.h.s. It is defined as:
FIRST can be applied to any r.h.s., and returns a set of terminal symbols.
Thus, if ![]() is the current non-terminal (ie. leftmost in the current
sentential form), and a is the next symbol on the input, then we
want to look at the r.h.s. of the production rules for
is the current non-terminal (ie. leftmost in the current
sentential form), and a is the next symbol on the input, then we
want to look at the r.h.s. of the production rules for ![]() and choose
the one whose FIRST set contains a.
and choose
the one whose FIRST set contains a.
FOLLOW is used only if the current non-terminal can derive
![]() ; then we're interested in what could have followed it in
a sentential form. (NB: A string can derive
; then we're interested in what could have followed it in
a sentential form. (NB: A string can derive ![]() if and only
if
if and only
if ![]() is in its FIRST set.)
is in its FIRST set.)
The ``![]() '' is a symbol which is used to mark the end of the input tape.
'' is a symbol which is used to mark the end of the input tape.
FOLLOW can be applied to a single non-terminal only, and returns a set of terminals.
Thus, if ![]() is the current non-terminal, a is the next symbol
on the input, and we have a production rule for
is the current non-terminal, a is the next symbol
on the input, and we have a production rule for ![]() which allows it to
derive
which allows it to
derive ![]() , then we apply this rule only if a is in
the FOLLOW set for
, then we apply this rule only if a is in
the FOLLOW set for![]() .
.
FIRST and FOLLOW help us to pick a rule when we have a choice between
two or more r.h.s. by predicting the first symbol that each r.h.s. can
derive. Even if there is only one r.h.s. we can still use them to
tell us whether or not we have an error - if the current input symbol
cannot be derived from the only r.h.s. available, then we know
immediately that the sentence does not belong to the grammar, without
having to (attempt to) finish the parse.