Non-Deterministic Finite-State Automata

In order to try and understand how lex builds a scanner, we will construct a formal model of the scanning process. This model should take characters one-by-one from the input, and identify them with particular patterns which match up with a regular expression.

The standard model used is the finite-state automaton. We can convert any definition involving regular expressions into an implementable finite automaton in two steps:

Regular expression $\longleftrightarrow$ NFA $\longleftrightarrow$ DFA

A non-deterministic finite-state automaton (NFA) consists of:

• An alphabet 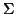$\Sigma$ of input symbols
• A set of states, of which we distinguish:
  • a unique start state, usually numbered ``0''
  • a set of final states
• A transition relation which, for any given state and symbol gives the (possibly empty) set of next states

We can represent a NFA diagrammatically using a (labelled, directed) graph, where states are represented by nodes (circles) and transitions are represented by edges (arrows).

The purpose of an NFA is to model the process of reading in characters until we have formed one of the words that we are looking for.

How an NFA operates:

• We begin in the start state (usually labelled 0) and read the first character on the input.

• Each time we are in a state, reading a character from the input, we examine the outgoing transitions for this state, and look for one labelled with the current character. We then use this to move to a new state.
  • There may be more than one possible transition, in which case we choose one at random.
  • If at any stage there is an output transition labelled with the empty string, 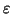$\varepsilon$, we may take it without consuming any input.
• We keep going like this until we have no more input, or until we have reached one of the final states.

• If we are in a final state, with no input left, then we have succeeded in recognising a pattern.

• Otherwise we must backtrack to the last state in which we had to choose between two or more transitions, and try selecting a different one.

Basically, in order to match a pattern, we are trying to find a sequence of transitions that will take us from the start state to one of the finish states, consuming all of the input.

The key concept here is that: every NFA corresponds to a regular expression

Moreover, it is fairly easy to convert a regular expression to a corresponding NFA. To see how NFAs correspond to regular expressions, let us describe a conversion algorithm.