Converting a NFA to a Regular Expression

The last theorem actually yields an algorithm for converting a NFA to a regular expression. The proof was by induction; we can transform this into a recursive function where the recursion is based on an integer argument.

We note that the induction step tells us that to calculate the language $L(p,q,K+1)$ for any $K > 1$, it will either be:

-

the language $L(p,q,K)$, or

-

the language $(L(p,K,K).L(K,K,K)*.L(K,q,K))$.

If we represent this ``or'' by the union operation, we then have a recursive definition of $L(p,q,K+1)$ in terms of languages of the form $L(\_,\_,K)$.

The base case is where $K=1$. As we have seen in the proof of Kleene's theorem, these machine components correspond to one-step transitions in the FSA, and the equivalent regular expressions are thus just the symbols which cause those transitions.

Based on this we can define function L, which takes three numbers as arguments and returns a regular expression, as follows:

regular-expression L(int I, int J, int K)
{
if (K==1)
return $\{a \;\mid\;$ there is an `$a$` transition between states $I$ and $J\}$
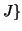
else
return L(p,q,K-1) | (L(p,K-1,K-1).L(K-1,K-1,K-1)*.L(K-1,q,K-1));
}

Given any FSA with $N$ states altogether, where $S$ is the start state and $F$ is the final state, we convert it to a regular expression by calling the function L(S,F,N+1)