Deterministic Finite-State Automata

NFAs are useful, in that they are easily constructed from regular expressions, and give us some kind of computational idea of how a scanner might work. However, since they involve making decisions, and backtracking if that decision was wrong, they are not really suitable for implementation using conventional programming languages.

Instead, we use a Deterministic Finite-State Automaton (DFA) which is a special case of a NFA with the additional requirements that:

1. There are no transitions involving $\varepsilon$
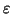
2. No state has two outgoing transitions based on the same symbol

Thus, when we are in some state in a DFA, there is no choice to be made; the operation of a DFA can very easily be converted into a program.

It is vital to note that: every NFA can be converted to an equivalent DFA

We will define an algorithm to do this, for arbitrary NFAs; the basic idea here is that sets of states in the NFA will correspond to just one state in the DFA.