



Next: DFA minimisation
Up: Deterministic Finite-State Automata
Previous: Deterministic Finite-State Automata
Contents
We merge together NFA states by looking at them from the point of view of the input
characters:
- From the point of view of the input, any two states that are connected by an
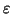 -transition may as well be the same, since we can move from one to the other without
consuming any character. Thus states which are connected by an
-transition may as well be the same, since we can move from one to the other without
consuming any character. Thus states which are connected by an 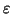 -transition will
be represented by the same states in the DFA.
-transition will
be represented by the same states in the DFA.
- If it is possible to have multiple transitions based on the same symbol, then we can
regard a transition on a symbol as moving from a state to a set of states (ie. the
union of all those states reachable by a transition on the current symbol). Thus these
states will be combined into a single DFA state.
To perform this operation, let us define two functions:
- The
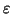 -closure function takes a state and
returns the set of states reachable from it based on (one or more)
-closure function takes a state and
returns the set of states reachable from it based on (one or more)
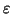 -transitions. Note that this will always include the
state tself. We should be able to get from a state to any state in
its
-transitions. Note that this will always include the
state tself. We should be able to get from a state to any state in
its 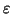 -closure without consuming any input.
-closure without consuming any input.
- The function move takes a state and a character, and
returns the set of states reachable by one transition on
this character.
We can generalise both these functions to apply to sets of states by
taking the union of the application to individual states.
Eg. If A, B and C are states, move({A,B,C},`a') = move(A,`a') 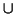 move(B,`a')
move(B,`a') 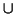 move(C,`a').
move(C,`a').
The Subset Construction Algorithm
- Create the start state of the DFA by taking the
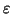 -closure of the start state of the NFA.
-closure of the start state of the NFA.
- Perform the following for the new DFA state:
For each possible input symbol:
- Apply move to the newly-created state and the input symbol; this
will return a set of states.
- Apply the
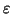 -closure to this set of states, possibly resulting in a new set.
-closure to this set of states, possibly resulting in a new set.
This set of NFA states will be a single state in the DFA.
- Each time we generate a new DFA state, we must apply step 2 to
it. The process is complete when applying step 2 does not yield any
new states.
- The finish states of the DFA are those which contain any of the
finish states of the NFA.




Next: DFA minimisation
Up: Deterministic Finite-State Automata
Previous: Deterministic Finite-State Automata
Contents
James Power
2002-11-29
![]() move(B,`a')
move(B,`a') ![]() move(C,`a').
move(C,`a').